Кривые Безье для ваших игр: учебник

Мы все знаем что такое кривая. Вот несколько примеров.
Кривые Безье очень просты в использовании, и могут описывать многие формы. Кривые Безье широко используются для представления символов в шрифтах, и форм конструкций транспортных средств. Кривые Безье также используются в редакторах векторной графики для представления различных кривых, и в инструментах 3D-анимации для представления анимационных кривых.
В играх кривые Безье иногда полезны для описания пути: гоночный путь на трассе в гоночной игре, или линии в играх с рисованием линий, таких как Flight Control, или зацикленная траектория парения бабочки, что что живет в мире RPG.

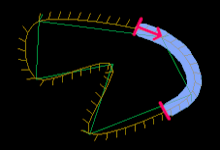

Кривые Безье так популярны, потому что их математическое описания очень компактно, интуитивно понятно и элегантно. Их легко вычислить, легко использовать в более высоких измерениях (3D и выше), и могут быть соединены вместе, чтобы представить любую форму какую вы только можете себе представить.
В этом руководстве я дам вам инструкции, необходимые для реализации алгоритмов, чтобы вы смогли использовать кривые Безье в своих играх.
Математическое описание
Начнем с математики. Математически мы можем описать кривую Безье на функцию. Функция принимает параметр 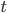 . Значение функции есть точка на кривой; она зависит от параметра
. Значение функции есть точка на кривой; она зависит от параметра 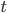 , и от множества точек, называемых контрольными точками. Первая и последняя контрольные точки являются концами кривой. Как правило, кривая не проходит через другие контрольные точки.
, и от множества точек, называемых контрольными точками. Первая и последняя контрольные точки являются концами кривой. Как правило, кривая не проходит через другие контрольные точки.
Значение 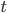 может колебаться от 0 до 1. Значение 0 соответствует начальной точке кривой, значение 1 соответствует конечной точке кривой. Значения в промежутке соответствуют остальным точкам на кривой.
может колебаться от 0 до 1. Значение 0 соответствует начальной точке кривой, значение 1 соответствует конечной точке кривой. Значения в промежутке соответствуют остальным точкам на кривой.
Вот пример простейшего типа кривой Безье, отрезок:
А вот сокращенное обозначение для двух уравнений, которые дают раздельные координаты:

Точки 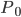 и
и 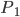 являются контрольными точками. Когда
являются контрольными точками. Когда 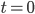 , правая часть уравнения равна первой контрольной точке - началу отрезка. Когда
, правая часть уравнения равна первой контрольной точке - началу отрезка. Когда 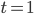 , получаем точку
, получаем точку 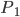 , вторую контрольную точку - конец отрезка.
, вторую контрольную точку - конец отрезка.
Для более интересных форм нам нужно больше контрольных точек. Количество контрольных точек определяет степень кривой. Две контрольные точки необходимы для линейных (первая степень) кривых, таких как отрезок выше. Для второй степени, или квадратичных кривых, нам нужны три контрольные точки.
Вот формула:
Кубические кривые (или кривые третьей степени) являются наиболее часто используюемыми, и поэтому в данном руководстве мы будем обсуждать именно кубические кривые. Для их построения требуется четыре контрольные точки, и возможно вы уже хорошо знакомы с их использованием в пакетах векторной графики (да, те самые кружочки которые используются для изменения формы кривых в программах Freehand или Inkscape и есть нашими контрольными точками).
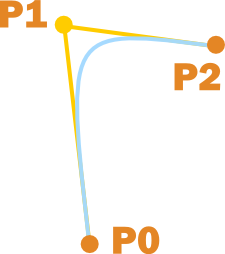
Желтые линии протянуты в том же направлении, что и касательные на концах кривой. Чем дальше расположены эти желтые сегменты, тем сильнее "натянута" кривая по направлению касательных.
Формула для кубических кривых Безье:
Вы вряд ли будете нуждаться в более высоких степенях кривой. Если это так, то формула проста, но требует некоторых знаний биномиальные коэффициентов. Вы можете найти подробности в одном из источников в конце статьи.
Случаи
В геометрии всегда найдется больше проблем, чем вы сначала могли подумать, что может привести к длительному поиску ошибок.
Вот правильные 2D кривые Безье:
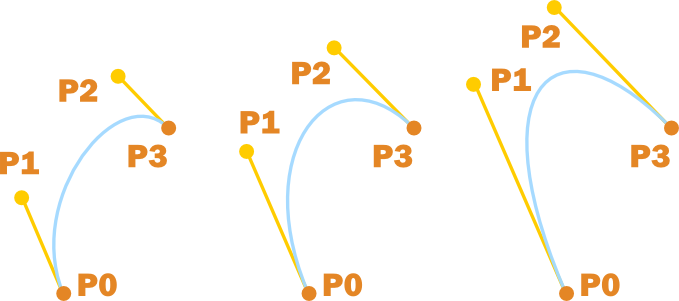
Все конечные точки на одинаковом расстоянии друг от друга. 1. Кривая без перегиба, залома или петли. 2. Кривая с перегибом, без заломов или петель. 3. Кривая с заломом. 4. Кривая с петлей. 5. Прямая линия. (В точке перегиба кривая меняет направления сгиба)
Вырожденный случай 5 является самым сложным. Могут быть следующие варианты:
- нет перекрытий
- кривая заламывается дважды на одном или обоих концах
- кривая заламывается трижды тройка где-то между концами
Существует шестой случай, когда все четыре контрольные точки совпадают: в результате кривая вырождается в одну точку. Обратите внимание, что кривая не вырождается в точку когда только конечные точки совпадают - все четыре контрольные точки должны совпадать. Кому интересны технические подробности могут почитать A Geometric Characterization of Parametric Cubic Curves (1.6 MB PDF) авторов Stone и De Rose. Статья Inflection points of a cubic Bezier объясняет, как вычислить точки перегиба, а также предоставляет интерактивные апплеты Java для наглядной иллюстрации.
В 3D, петли и переломы доставляют меньше проблем, так как они проявляются только в том случае, когда все точки лежат в одной плоскости. В 3D всегда можно изменить направление движения прямой (особенно для таких случаев как 2, 4 и 5).
При реализации алгоритмов кривых Безье, хорошо подумайте о целесообразности применения этого вида кривых к конкретному случаю, и всегда проверяйте на корректность работы алгоритма. Будьте особенно осторожны с контрольными точками - при их совпадении может возникнуть ситуация с нормализацией нулевого вектора, что в свою очередь может привести к падению программы.
Реализация
Математическую формулу несложно перевести в код. Ниже приводиться реализация алгоритма, в которой уже произведена некоторая оптимизация путем сохранения и повторного использования промежуточных результатов.
Код приводится на языке C#, но перевести на Java, C + + и большинство других языков не должно принести особых проблем.
(Следующие функции будут работать и в 2D, если Vector3 заменить на Vector2.)
Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3) { float u = 1 – t; float tt = t*t; float uu = u*u; float uuu = uu * u; float ttt = tt * t; Vector3 p = uuu * p0; //first term p += 3 * uu * t * p1; //second term p += 3 * u * tt * p2; //third term p += ttt * p3; //fourth term return p; } |
Рисование кривых Безье
Теперь у нас есть способ вычисления точки на кривой Безье, нам нужен способ рисования кривой.
Для изображений, самый простой подход заключается в использовании итерирования 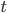 для расчета требуемых точек:
для расчета требуемых точек:
for (int i = 0; i <= SEGMENT_COUNT; ++i) { t = i / (float)SEGMENT_COUNT; Vector3 pixel = CalculateBezierPoint(t, p0, p1, p2, p3); DrawPixel(pixel); //assume this function can handle Vector3 } |
Этот подход страдает от следующих проблем:
- очень сложно угадать подходящий шаг для приращения
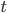 ;
; - некоторые пиксели могут быть нарисованы много раз;
- некоторые пиксели могуть быть пропущены.
Более продвинутые алгоритмы используют адаптивный прирост 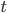 чтобы преодолеть эти проблемы. Сглаживание (antialiasing) кривой даст вообще класный результат, делая кривую очень гладкой и четкой. Хорошим источником для рисования кривых (и еще куча полезных тем) является Computer Graphics and Computer Modelling от David Salomon.
чтобы преодолеть эти проблемы. Сглаживание (antialiasing) кривой даст вообще класный результат, делая кривую очень гладкой и четкой. Хорошим источником для рисования кривых (и еще куча полезных тем) является Computer Graphics and Computer Modelling от David Salomon.
Более простой альтернативой является рисовать линии, а не пикселей. Этот метод также более подходящий для рисования кривых с помощью графического оборудования.
q0 = CalculateBezierPoint(0, p0, p1, p2, p3); for (int i = 1; i <= SEGMENT_COUNT; ++i) { t = 1 / (float)SEGMENT_COUNT; q1 = CalculateBezierPoint(t, p0, p1, p2, p3); DrawLine(q0, q1); q0 = q1; } |
Так как теперь нам не нужно волноваться о пропуске пикселей, можно выбрать больший прирост и снизить нагрузку на отрисовку. Но все же трудно выбрать приращение должным образом.
Существует другой алгоритм, использующий рекурсивные разбиения. Как правило, он дает меньше точек отрисовок на тот же уровень точности, чем в предыдущем алгоритме. Тем не менее, он не обрабатывает все кривые с перегибами или петлями должным образом, и не должен использоваться, если возможно появление таких случаев.
Вот алгоритм:
- Стартуем в конечных точках: кривая указывает на
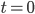 и
и 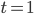 .
. - Рассчитать точку по середине отрезка (
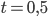 в первой итерации).
в первой итерации). - Если угол между двумя получеными отрезками меньше порогового значения, тогда добавляем полученую точку в отрисовку. Дальше рекурсивно повторять для каждой половинки кривой. Алгоритм останавливается когда дальнейшее разбиение невозможно, или отрезки достигли минимальной длины.
На рисунке ниже показан рабочий пример.
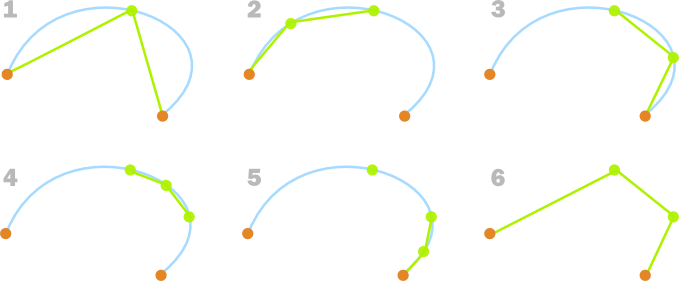
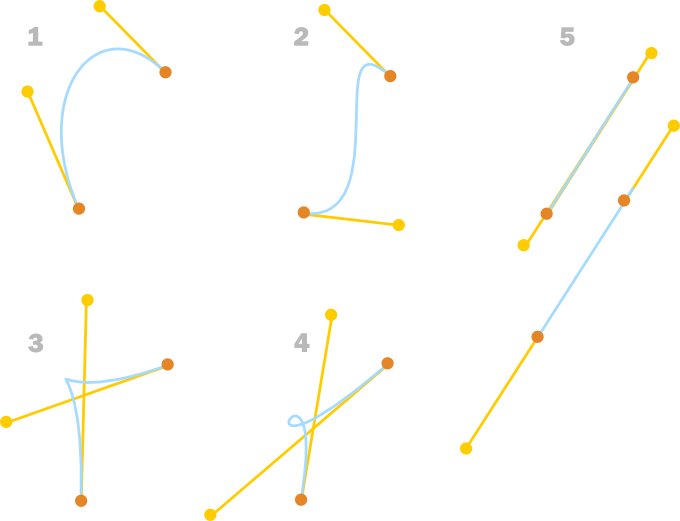
1. Начнем с двух конечных точек и точкой между ними. Мы проверяем угол, образованный между двумя отрезками. Он достаточно мал, поэтому мы добавим между ними точку отрисовки. 2. Затем мы делаем то же самое для левой части кривой.В этом случае угол достаточно велик, так что мы не добавляем точку, и не разбиваем дальше. 3. Мы делаем то же самое для правой части кривой. В этом случае угол достаточно мал, поэтому мы добавляем новые точки для отрисовки, и развиваем отрезок. 4. И 5. Мы делаем то же самое для двух половинок на предыдущем шаге. В каждом случае угол достаточно велик, так что новые точки не добавляются, разбиение также не нужно. 6.Окончательный набор точек используется для рисования кривой.
Ниже приведен код рекурсивного алгоритма. Хитрость в том, чтобы вставлять точки в нужном месте в списке так, что они остаются в правильном для отрисовки порядке. Мы проверяем скалярное произведения нормированных сегментов, вместо проверки угла непосредственно. Именно поэтому для сравнения используется >, вместо < как если бы мы проверяли углы напрямую.
//returns the number of points added. int FindDrawingPoints(float t0, float t1, int insertionIndex, List pointList) { tMid = (t0 + t1) / 2; p0 = bezierCurve(t0); p1 = bezierCurve(t1); if (p0 – p1.sqrMagnitude < MINIMUM_SQR_DISTANCE) { return 0; } pMid = bezierCurve(tMid); leftDirection = (p0 – pMid).Normalised; rightDirection = (p1 – mMid).Normalised; if (Dot(leftDirection, rightDirection) > threshold) { int pointsAddedCount = 0; pointsAdded += FindDrawingPoints(t0, tMid, insertionIndex, pointList) pointList.insert(insertionIndex + pointsAdded, pMid); pointsAdded++; pointsAdded += FindDrawingPoints(tMid, t1, insertionIndex + pointsAdded, pointList); return pointsAdded; } return 0; } |
Следующая функция демонстрирует вызов рекурсивной функции:
void FindPoints() { List pointList = new List(); p0 = bezierCurve(0); p1 = bezierCurve(1); pointList.Add(p0); pointList.Add(p1); int pointsAdded = FindPoints(0, 1, 1, pointList); assert(pointsAdded + 2 == pointsList.Count); //sanity check } |
Несколько замечаний:
- Проверка на минимальное расстояние необходима для предотвращения проблем с нормализацией очень коротких векторов. Она также предотвращает ненужные вычисления.
- Пороговое значение на удивление близко к -1. Для старта неплохо начать с -0,99.
- Алгоритм не очень хорошо работает для кривых, которые содержат перегибы или петли. Ниже приведен пример того, что может произойти, если применить его к кривой с перегибом.
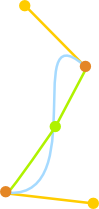
Пример, в котором алгоритм даст плохой результат. В этом случае угол превышает допустимый порог, так что никаких разбиений не будет происходить. Результат не сильно похож на желаемую кривую.
Склейка кривых вместе: пути Безье
Когда мы хотим построить сложную кривую, у нас есть два варианта:
- использовать одну кривую Безье с высокой степенью;
- разделить кривую на более мелкие сегменты, и использовать кривые Безье низкой степени для каждого сегмента.
Последний тип кривой называется пути Безье. Пути Безье, как правило, более просты и эффективны в использовании, чем кривые высокой степени, поэтому именно этот метод здесь и описывается.
Приведенная здесь реализация является лишь одной из многих возможных. Мы определим класс, который создает список контрольных точек кривых Безье, которые составляют путь Безье. Поскольку сегменты связаны концом-к-концу, начальная и конечная точка соседних кривых совпадают, таким образом мы можем избежать дублирования точек. На рисунке показан пример пути Безье составленого из четырех кривых Безье. В этом случае, список содержит 13 точек, как показано на рисунке слева.
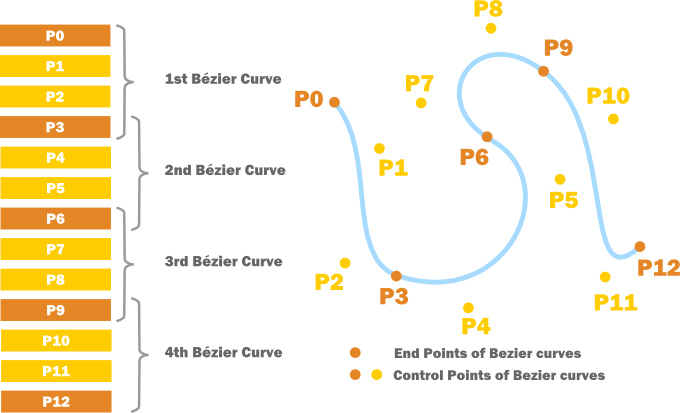
Если мы решим построить кривую с отрезками, то хорошим решением будет кешировать конечные точки отрезков, и обновлять их по мере изменения кривой. Следующий алгоритм вычисляет все точки отрисовки (конечные точки отрезков).
class BezierPath { List controlPoints; Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3) {...} List GetDrawingPoints() { List drawingPoints = new List(); for(int i = 0; i < controlPoints.Count - 3; i+=3) { Vector3 p0 = controlPoints[i]; Vector3 p1 = controlPoints[i + 1]; Vector3 p2 = controlPoints[i + 2]; Vector3 p3 = controlPoints[i + 3]; if(i == 0) //Only do this for the first endpoint. //When i != 0, this coincides with the end //point of the previous segment { drawingPoints.Add(CalculateBezierPoint(0, p0, p1, p2, p3)); } for(int j = 1; j <= SEGMENTS_PER_CURVE; j++) { float t = j / (float) SEGMENTS_PER_CURVE; drawingPoints.Add(CalculateBezierPoint(t, p0, p1, p2, p3)); } } return drawingPoints; } } |
Данный рекурсивный алгоритм легко адаптируется для получения промежуточных точек. Пример вы можете найти в прилагаемом к статье коде.
Последние советы
При реализации путей Безье, вы можете сделать вашу жизнь намного проще, выполнив следующие действия:
- Включить отладку режимов для рисования контрольных точек, конечных точек Безье, рисование точек и касательных.
- Вывести число точек отрисовки и контрольных точек: благодаря этому вы всегда сможете проверить сколько точек генерирует алгоритм, и вменяемость этого количества.
Ну и напоследок - кривые Безье это очень круто, но не стоит использовать их везде, особенно для представления коротких, практически прямых линий.
- Большинство 3D движков требуют использовать короткие прямые линии для рендеринга кривых, поэтому вы должны точно представлять себе ценность внедрения отрисовки кривых Безье.
- Когда движение находится под контролем физики, соответственно резкие изменения скорости и направления практически отсутсвуют. Объекты, как правило, перемещаются путем изменения силы, действующей на объект, и благодаря этому их скорость не может измениться мгновенно. Таким образом, любое движение сглаживается автоматически: любой объект следующий вдоль соединенных прямых линий будет автоматически следовать сглаженому пути - в кривых Безье нет никакой надобности.
Скачать
- Bezier Curves (64 KB, Unity 3D Project, zipped)
- BezierPath.cs (C# source code file)
Статья является переводом, ссылка на источник - Bezier Curves for your Games: A Tutorial.
Если вы заметите какие либо неточности в переводе - просьба сообщать об этом письмом на адрес указаный внизу страницы.

![[x, y] = (1 - t)P_0 + tP_1](http://3d-orange.com.ua/wp-content/plugins/latex/cache/tex_35838694cefa779d78af1dde3cd28333.gif)
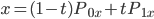
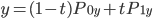
![[x, y] = (1 - t)^2P_0 + (1 - t)tP_1 + t^2P_2](http://3d-orange.com.ua/wp-content/plugins/latex/cache/tex_cb92fc17fb9713911ed8ca94b03ea7d4.gif)
![[x, y] = (1 - t)^3P_0 + 3(1 - t)^2tP_1 + 3(1 - t)t^2P_2 + t^3P_3](http://3d-orange.com.ua/wp-content/plugins/latex/cache/tex_edbb2309cda8b110ea07503c601c6780.gif)
Данный туториал подходит для Гейм Мейкера?
Здравствуйте!
К сожалению я не знаком со средой Game Maker, но если в ней есть язык программирования - то думаю можно адаптировать код.
По-моему в формуле для квадратичных кривых ошибка. Второе слогаемое должно быть 2 * (1 - t) * t * P1.
Ещё один вопрос, достойный внимания. Если у вас кривая безье третьего порядка, по которой движется объект, и надо, чтобы он всегда был направлен по направлению движения, то в качестве точки взгляда (функция LookAt в Unity) можно использовать кривую второго порядка для точек P1, P2, P3. Коррекция нужна только когда t приближается к 1, т.к. сам объект и точка куда он смотрит сильно сближаются.
Большое спасибо за подробное описание. Очень полезная статья.
[...] статью на gamedev.ru, а потом в комментариях к статье нашел другую и неожиданно обрел знание: как работают кривые Безье и [...]
Здравствуйте автор! Спасибо статью! Можно вам задать такой вопрос так как думаю что вы скорее всего сталкивались с этим, так вот, как нарисовать линию в 3d пространстве? В 2d я уже разобрался вроде(алгоритм Брезенхэма), думаю что можно как то его модифицировать для дополнительной оси z, но пока что то не получается. Нужно мне это для описания полета снаряда.
С уважением Рашид!
Здравствуйте Рашид!
Все зависит от того каким способом вы собираетесь отрисовывать 3D.
Если будете использовать какой-то из общепринятых 3D API (OpenGL, Direct3D) - у них есть необходимый Вам функционал.
Если же стоит задача отрисовывать 3D-линии программно - то здесь тоже нет ничего сложного, Вам лишь нужно посчитать координаты Ваших 3-хмерных точек,
затем спроецировать их на экранную плоскость и отрисовать готовые 2D-линии.
q0 = CalculateBezierPoint(0, p0, p1, p2, p3);
for (int i = 1; i <= SEGMENT_COUNT; ++i)
{
t = 1 / (float)SEGMENT_COUNT;
q1 = CalculateBezierPoint(t, p0, p1, p2, p3);
DrawLine(q0, q1);
q0 = q1;
}
Исправте 1 на i пожалуйста.